Pengertian Kesebangunan
Kesebangunan merupakan sebuah bangun datar di mana sudut – sudutnya mempuntai kesesuaian yang sama besarnya. Dan juga panjang sisi – sisi sudutnya juga bersesuai dengan mempunyai sebuah perbandingan yang sama.
Dengan kata lain, kesebangunan merpuakan dua buah bangun yang memiliki sudut serta panjang sisi yang sama.
Kesebangunan pada umumnya dilambangkan dengan menggunakan simbol notasi ≈.
Dua Bangun Datar yang Sebangun

Bangun datar di atas sebangun dengan:
Dua bangun datar di atas adalah dua bangun yang sebangun, dengan memiliki beberapa sifat seperti yang ada di bawah ini:
1. Pasangan Sisi -sisinya yang Bersesuaian mempunyai Perbandingan Nilai yang Sama. Berikut penjelasannya:
- Sisi AD dan KN merupakan AD/KN = 3/6 = 1/2
- Sisi AB dan KL merupakan AB/KL = 3/6 = 1/2
- Sisi BC dan LM merupakan BC/LM = 3/6 = 1/2
- Sisi CD dan MN merupakan CD/MN = 3/6 = 1/2
Sehingga, dari uraian di atas dapat kita simpulkan bahwa AD/KN = AB/KL = BC/LM = CD/MN.
2. Besar Sudut – Sudut yang Bersesuaian Sama, yaitu:
∠A = ∠P; ∠B = ∠Q; ∠C = ∠R
Jika kita bicara pada konteks bangun datar, selain perbandingan yang memiliki panjang sama, supaya dapat dikatakan sebangun, dua bangun datar tersevut harus memenuhi dua syarat di bawah ini:
- Sudut-sudut yang bersesuaian sama besar
- Sisi-sisi yang bersesuaian memiliki perbandingan yang sama
Pengertian Kekongruenan
Kekongruenan merupakan dua buah bangun datar yang di mana kedua bangunnya sama – sama memiliki bentuk dan juga ukuran yang sama.
Kekongruenan ini biasa dilambangkan dengan pemakaian simbol ≅.
Perhatikan contoh di bawah ini:
1. Dua Bangun Datar yang Kongruen
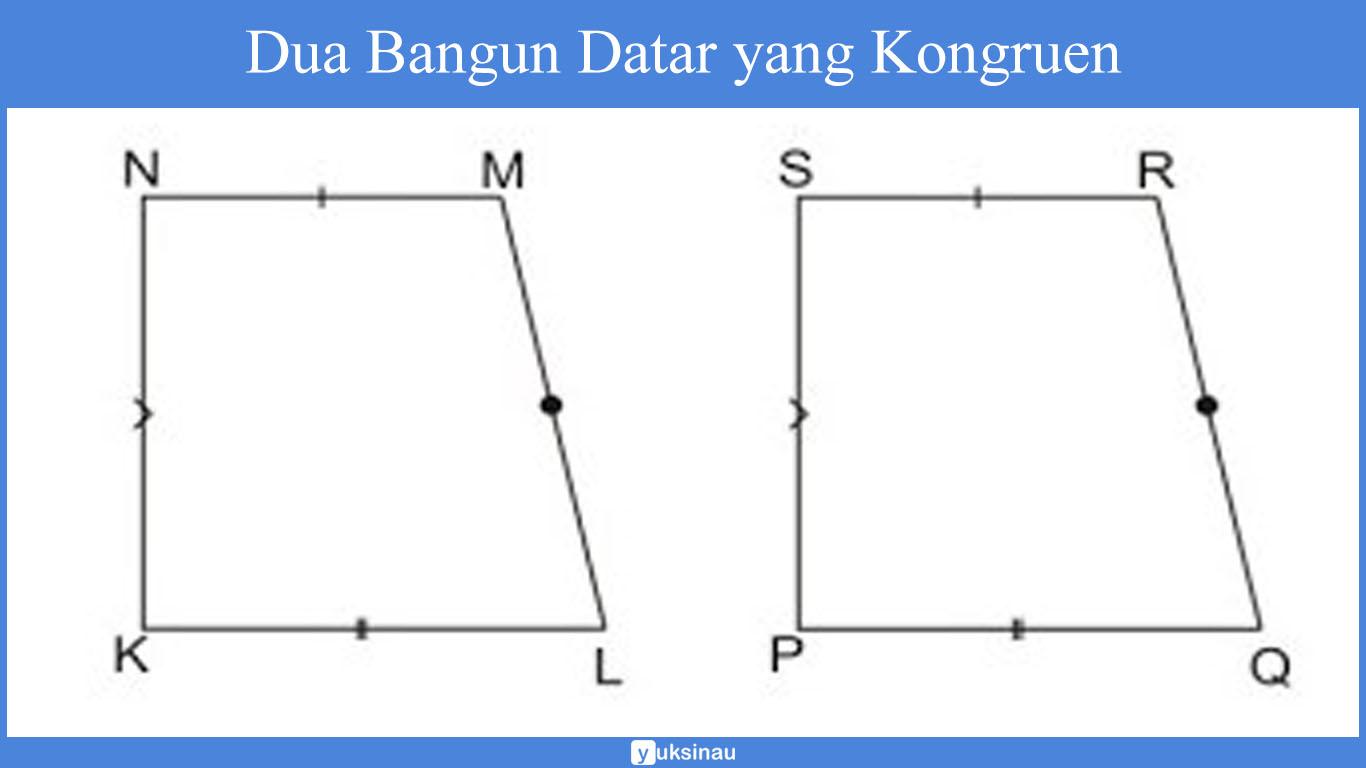
Pada kedua bangun di atas adalah bangun yang kongruen, karena panjang KL = PQ, Panjang LM = QR, panjang MN = RS, panjang NK = SP maka oleh karena itu, pada bangun KLMN dan PQRS dapat dikatakan adalah kongruen karena memiliki bentuk dan ukuran yang sama.
2. Dua Segitiga yang Kongruen
Secara geometris, dua segitiga yang kongruen merupakan dua buah bangun segitiga yang saling menutupi dengan tepat.
Sifat dari kedua bangun segitiga kongruen tersebut antara lain yakni
. Pasangan sisi yang bersesuaian merupakan sama panjang.
b. Sudut yang bersesuaian merupakan sama besar.
Segitiga bisa disebut sebagai kongruen mana kala bisa memenuhi beberapa syarat seperti berikut:
a. Tiga Sisi yang Bersesuaian Sama Besar (sisi, sisi, sisi)

Berdasarkan gambar dari segitiga ABC serta segitiga PQR di atas, diketahui jika keduanya mempunyai panjang AB = PQ, panjang AC = PR, serta panjang BC = QR.
b. Sudut dan Dua Sisi yang Bersesuaian Sama Besar (sisi, sudut, sisi)

Berdasarkan dari gambar bangun segitiga ABC serta segitiga PQR di atas, diketahui jika kedua bangunnya memiliki sisi AB = PQ, ∠B = ∠Q, dan juga sisi BC = QR
c. Satu Sisi Apit dan Dua Sudut yang Bersesuaian Sama Besar (sudut, sisi, sudut)

Dua bangun yang sama persis memang disebut sebagai kongruen. Namun, secara formal, dalam konteks bangun datar, jika terdapat dua buah bangun datar bisa disebut kongruen apabila dapat memenuhi dua syarat, yakni:
- Sudut-sudut yang bersesuaian sama besar
- Sisi-sisi yang bersesuaian sama panjang
Perbedaan Kesebangunan dan Kekongruenan
Hal mendasar yang membedakan kongruen dan sebangun yaitu:
Bangun dikatakan kongruen jika sisi-sisi yang bersesuaian harus sama panjang. Sementaa jika bangun dikatakan sebangun apabila perbandingan sisi-sisi yang bersesuaian harus sama besar.
Sehingga dapat kita simpulkan bahwa, seluruh bangun yang kongruen sudah pasti sebangun, namun jika sebangun belum tentu kongruen.
Contoh Soal Dan Pembahasan
Berikut akan kami berikan contoh soal sekaligus pembahasannya mengenai Kongruen dan Kesebangunan. Perhatikan baik-baik ya..
Soal 1.
Gilang memiliki tinggi badan 150 cm. Gilang kemudian berdiri pada titik yang memiliki jarak 10 m dari suatu gedung.
Ujung bayangan dari Gilang berimpit dengan ujung bayangan gedung. Jika panjang bayangan Febri yaitu 4 m, maka tinggi gedung tersebut yaitu ….
Jawab:

Kita perhatikan terlebih dahulu pada gambar bangun segitiga ABE dan segitiga ACD!
Dilihat dair prinsip kesebangunan, maka bisa kita dapatkan jika EB/DC = AB/AC, sehingga:

Maka kita ketahui hasilnya yakni: DC = 5,24 m.
Soal 2:
Perhatikan gambar bangun datar di bawah ini:

Berdasarkan gambar bangun persegi panjang ABCD dan PQRS di atas ialah sebagun. Sehingga hitunglah:
a. Berapa panjang PQ?
b. Berapa luas dan juga keliling persegi panjang PQRS?
Jawab:
a. Perbandingan sisi AB dengan AD bersesuaian dengan sisi PQ dan PS sehingga:
PQ/ PS = AB/AD
PQ/6 = 16/4
PQ = 16×6/ 4 = 96/4 = 24 cm.
Sehingga diketahui panjang PQ yaitu 24 cm.
b. Mencari luas dan juga keliling persegi panjang PQRS:
Luas persegi panjang menggunakan rumus: panjang x lebar, sehingga:
Luas persegi panjang PQRS yakni:
PQ x PS = 24 cm x 6 cm = 144 cm2
Keliling persegi panjangnya yakni:
Keliling persegi panjang PQRS = PQ + QR + RS + SP = 24 cm + 6 cm + 24 cm + 6 cm = 60 cm.
Soal 3. SOAL UN MATEMATIKA SMP 2016
“Lebar Sungai”
Andi ingin mengetahui lebar sungai. Di seberang sungai terdapat sebuah pohon. Untuk itu dia menancapkan tongkat sehingga berada pada posisi A, B, C, dan D dengan ukuran seperti pada gambar.

Andi ingin mengukur lebar sungai dari tongkat D sampai pohon. Berapa lebar sungai tersebut?
A. 11 m
B. 12 m
C. 15 m
D. 16 m
Pembahasan:
Perhatikan sketsa berikut!

Lebar sungai dapat dihitung dengan memanfaatkan kesebangunan segitiga.
Lebar sungai = DP
DP/ AP = DC/AB
DP/ 4+DP = 6/8
8DP = 6 x (4 + DP)
8DP = 24 + 6DP
8DP – 6DP = 24
2DP = 24
DP = 24/2 = 12m
Sehingga, lebar sungai adalah= DP = 12 m.
Jawaban: B
Soal 4. Soal UN Matematika SMP/MTS Tahun 2010
Perhatikan gambar!

P dan Q merupakan titik tengah diagonal BD dan AC. Panjang PQ adalah .…
A. 5 cm
B. 4 cm
C. 3 cm
D. 2 cm
Jawab:
Rumus cepat untuk memperoleh panjang PQ yaitu dengan cara:
PQ = 1/2 (DC – AB)
PQ = 1/2(12 – 6)
PQ = 1/2 x 6
PQ = 3
Sehingga, jawabannya adalah C.
